Le strutture gerarchiche su database

Introduzione

Questo articolo vuole essere un piccolo approfondimento volto ad affrontare il problema della gestione di strutture gerarchiche su database, problema che meriterebbe una ampia discussione sul piano teorico e che viene affrontato nella pratica non soltanto in ambito web.

Il nostro primo passo sarà riuscire a focalizzare bene il problema, per poi proporre due delle possibili soluzioni teoriche, corredate da esempi implementati naturalmente in PHP e MySQL.

Inquadriamo il problema

Quando parliamo di struttura gerarchica, o di struttura ad albero, intendiamo un insieme di dati che hanno una qualche forma di "parentela". Al lato pratico gli esempi sono numerosissimi: pensiamo ad una bulletin board, in cui i messaggi sono raggruppati per thread (discussione); pensiamo ad un catalogo sul web di prodotti suddivisi per categorie, in cui ad esempio possiamo trovare il nostro disco fisso navigando attraverso le categorie "Informatica - Hardware - Hard disk - SCSI"; pensiamo ad una enciclopedia, in cui le informazioni sono suddivise per argomenti e sottoargomenti; pensiamo infine ad una struttura aziendale, in cui ogni impiegato ha un capo, il quale a sua volta avrà un proprio capo, e così via.

In figura 1 troviamo una rappresentazione grafica dell'ultimo esempio.

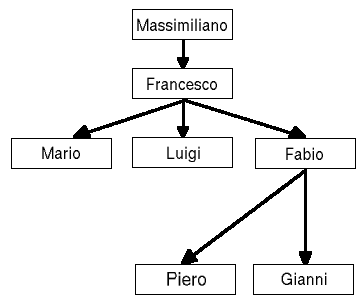
Tradurre uno qualsiasi di questi esempi in una tabella di database può risultare inizialmente ostico, ed il rischio è quello di progettare una struttura che risulterà poi scomoda da gestire. Le due soluzioni che andiamo ad affrontare in questa sede prendono il nome di Adjacency List Model, la soluzione più semplice, e di Modified Preorder Tree Traversal, soluzione più articolata e non immediata, proposta da Joe Celko e meglio conosciuto come "Nested Sets".

Prima soluzione: Adjacency List Model

Proviamo ad implementare la struttura aziendale vista nella figura 1 utilizzando l'approccio proposto dall'Adjacency List Model.

Dietro al nome altisonante di questo algoritmo si nasconde un'idea semplice e per alcuni versi elegante: ad ogni nodo è necessario associare un identificativo del nodo padre, mentre la radice dell'albero non avrà alcun padre.

Creiamo la tabella che conterrà i nostri dati:

CREATE TABLE personale(
    id_impiegato INT UNSIGNED NOT NULL AUTO_INCREMENT DEFAULT 1,
    id_capo INT UNSIGNED DEFAULT NULL,
    nome VARCHAR(50) NOT NULL,
    -- altri campi a piacere
    PRIMARY KEY(id_impiegato)
);

Il campo id_impiegato rappresenta la chiave primaria della tabella, mentre il campo id_capo dovrà contenere la chiave del rispettivo capo. La scelta di una chiave numerica AUTO_INCREMENT serve soltanto per semplificare l'esempio. La radice avrà come identificativo del padre il valore NULL.

Inseriamo la radice dell'albero:

INSERT INTO personale(nome) VALUES('Massimiliano');

Il primo impiegato prenderà i valori di default, quindi id_impiegato=1 ed id_capo=NULL (in sostanza è il capo).

Inseriamo un suo diretto dipendente:

INSERT INTO personale(id_capo, nome) VALUES(1, 'Francesco');

Essendo il campo id_impiegato un AUTO_INCREMENT, Francesco sarà identificato dal numero 2. Inseriamo i suoi sottoposti:

INSERT INTO personale(id_capo, nome) VALUES (2, 'Mario'), (2, 'Luigi'), (2, 'Fabio');

Dopo aver completato tutti gli inserimenti, la situazione sarà simile a quella proposta in figura 2:

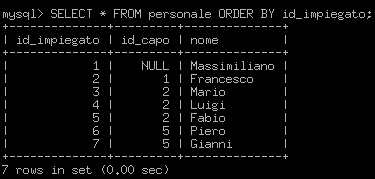
Operazioni sull'albero

Ora che abbiamo la struttura, sfruttiamo la libreria allegata per svolgere le operazioni che ci possono interessare. Dentro all'archivio zip troverete un file mysqlconnect.php con i parametri per la connessione a MySQL, da personalizzare ed un file adjacencylist.php che conterrà alcune funzioni per operare sull'albero.

Nota: per semplicità non sono stati inseriti controlli per gestire gli errori o tipi di dato non validi, per cui è opportuno utilizzare questa libreria soltanto a scopo di test. Inoltre abbiamo incluso del codice strettamente legato allo schema della tabella proposta nei paragrafi precedenti. Al lettore lasciamo la possibilitè di personalizzare questa libreria, fornendo magari il proprio feedback.

Primo esempio semplice: troviamo tutti i figli di un determinato nodo. Basta una query, ma per comodità utilizziamo comunque la nostra libreria. È necessario conoscere a priori l'identificativo del nodo di cui vogliamo trovare i figli:

<?php
// inclusioni necessarie
require_once 'adjacencylist.php';
require_once 'mysqlconnect.php';
// Cerco tutti i figli del nodo "Francesco" (ID=2)
$padre = 2;
echo '<pre>';
print_r(al_get_children($padre));
echo '</pre>';
?>

Se invece volessimo ottenere il percorso necessario per arrivare dalla radice ad una determinata foglia, dobbiamo utilizzare una funzione che chiama ricorsivamente una serie di query SELECT. Per fare ciò, ancora, ci serve conoscere il valore della chiave del nodo foglia. Proviamo ad esempio con Piero (ID=6):

<?php
require_once 'adjacencylist.php';
require_once 'mysqlconnect.php';
$nodo = 6; 
echo
'<pre>';
print_r(al_get_path($nodo));
echo
'</pre>';
?>

Il risultato sarà l'array contenente tutti i nodi necessari per arrivare da Massimiliano a Piero.

Da notare come, aumentando la profondità dell'albero, vada ad aumentare anche il numero di query. La ricorsività è necessaria in quanto questo modello non consente di effettuare l'operazione voluta con una sola query.

Nella libreria sono presenti due funzioni che servono per eliminare un nodo intermedio e per spostare un ramo da una parte all'altra dell'albero. Più ci addentriamo nell'utilizzo di questo sistema, più andiamo però a scoprire piccoli problemi.

Difetti nell'Adjacency List Model

Questo modello, nella sua versione più semplice, presenta numerosi punti "oscuri" che spesso vanno chiariti dal programmatore. L'impossibilità di ottenere il percorso completo dalla radice ad un nodo tramite una sola query è già un primo ostacolo che abbiamo risolto con qualche riga di PHP, ma a scapito delle prestazioni. Esistono poi altre anomalie strutturali nella tabella che abbiamo creato: non ci sono vincoli che ci garantiscano di non inserire cicli all'interno dell'albero, di non avere due radici (quindi due capi), di non avere riferimenti a se stessi.

Queste query INSERT portano alla luce questi problemi:

-- In questo modo abbiamo due capi
INSERT INTO personale (id_impiegato, id_capo) VALUES(1, NULL);
INSERT INTO personale (id_impiegato, id_capo) VALUES(2, NULL);
-- Esempio di ciclo
INSERT INTO personale (id_impiegato, id_capo) VALUES(3, 4);
INSERT INTO personale (id_impiegato, id_capo) VALUES(4, 3);
-- Riferimento a se stesso
INSERT INTO personale (id_impiegato, id_capo) VALUES(5, 5);

Oltre all'inserimento, anche la cancellazione presenta dei problemi. Immaginando di cancellare il nodo "Francesco" dalla tabella iniziale, avremo l'albero spezzato in due: da un lato Massimiliano nel ruolo del capo, dall'altra tutti i dipendenti che sono rimasti però senza un capo. La tabella va quindi sistemata per ricongiungere le due parti dell'albero: possiamo "promuovere" tutti i sottoposti di Francesco, facendoli dipendere direttamente da Massimiliano, oppure possiamo scegliere uno di questi e promuovere soltanto lui. Per implementare la prima soluzione basta una sola query:

UPDATE personale SET id_capo=1 WHERE id_capo=2;

Per poter effettuare una query del genere, dobbiamo però conoscere l'id del capo di Francesco, prima di rimuovere il suo record dalla tabella (soluzione adottata nella funzione al_delete_node() della libreria).

Se invece decidiamo di promuovere soltanto uno degli impiegati, ad esempio Mario (id=3), dovremo muoverci in questo modo:

UPDATE personale SET id_capo=1 WHERE id=3;
UPDATE personale SET id_capo=3 WHERE id_capo=2;

Nelle due figure che seguono, vediamo l'albero ricostruito in base alle due diverse strade adottate.

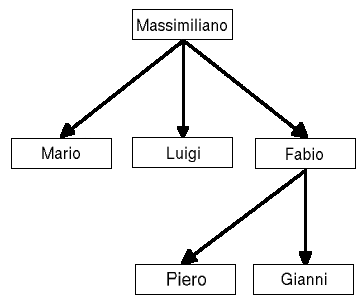
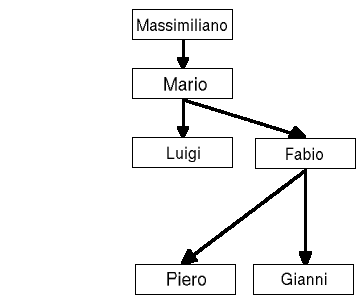
Conclusioni

La semplicità a volte si paga. Nel nostro caso si paga in termini di affidabilità o di prestazioni. Le considerazioni sulle possibili anomalie dell'Adjacency List Model mettono in luce la necessità di una nuova soluzione. Nella prossima parte dell'articolo prenderemo in esame il Modified Preorder Tree Traversal Algorith, più complicato in fase di implementazione iniziale, ma più performante ed affidabile e cercheremo infine di trovare qualche ulteriore spunto di riflessione.

Alla ricerca di una soluzione migliore

Dopo aver constatato che la prima soluzione proposta, quella effettivamente più intuitiva, si è rivelata inadatta al nostro scopo, proviamo ad affrontare il problema da un altro punto di vista.

L'approccio che andiamo a descrivere è stato suggerito da Joe Celko, uno dei personaggi più in vista nel mondo dei database, per cui ci rifaremo direttamente ai suoi insegnamenti, che ci arrivano tramite numerosi scritti, alcuni dei quali elencati nel paragrafo conclusivo.

Per comprendere meglio questa nuova soluzione, possiamo considerare la nostra struttura gerarchica non solo come un albero, ma piuttosto come una serie di insiemi e sottoinsiemi, da cui il nome "nested sets". In figura 5 troviamo una rappresentazione insiemistica della struttura aziendale proposta nella prima parte dell'articolo.

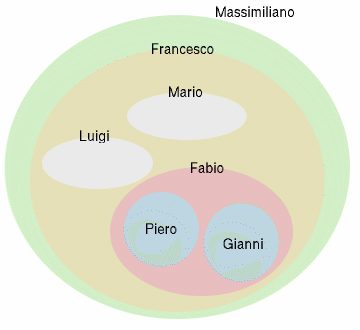
Naturalmente è sbagliato pensare ad una persona come ad un insieme. Si tratta invece, in questo esempio, di avere una visualizzazione semplice di chi è il capo (l'insieme più grande) e di chi sono i vari dipendenti (gli insiemi via via innestati).

Un ulteriore punto di vista, che servirà poi per implementare nella pratica questo nuovo approccio, consiste nel riprendere l'albero e scorrerlo completamente dalla radice, passando per i nodi intermedi, ai nodi foglia, per poi tornare alla radice. Ad ogni nodo associamo due etichette che conterranno un numero crescente. La numerazione parte dalla radice, in cui è necessario segnare la prima etichetta col numero 1. Si prosegue scendendo attraverso i livelli, marcando sempre la prima etichetta di ciascun nodo. Arrivando ai nodi foglia, non sarà più possibile scendere, per cui si andrà a marcare anche la seconda etichetta per poi risalire di un livello. Quando tutte le foglie sono state etichettate due volte, si risale via via fino alla radice.

L'ordine apparentemente strano di questi numeri ci fornisce però alcuni risultati che sono predicibili, grazie ai quali possiamo costruire delle query che tornano poi estremamente utili. Notiamo ad esempio che la radice è sempre marcata con il numero 1 e con il numero N*2, dove N è il numero totale dei nodi. Inoltre ogni nodo foglia è marcato con due numeri consecutivi.

La figura 6 rappresenta la solita struttura aziendale, aggiornata con le nuove etichette: consideriamo la prima etichetta quella di sinistra, mentre la seconda quella di destra.

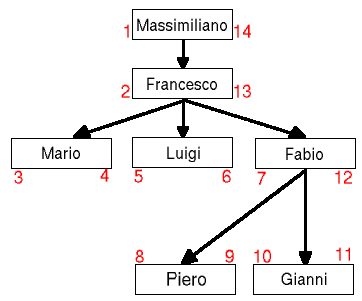
Il fatto di attraversare in questo modo l'albero, modificando il normale "ordine" dei nodi (che per altro non ne hanno uno definito), offre il nome all'algoritmo, ossia Modified Preorder Tree Traversal Algorithm.

Prepariamo la tabella

Ricreiamo ora la tabella che conterrà la nostra struttura aziendale, seguendo le indicazioni del nuovo approccio. Serviranno due nuove colonne per contenere i valori numerici delle due etichette:

CREATE TABLE personale(
    id INTEGER UNSIGNED AUTO_INCREMENT,
    nome VARCHAR(50) NOT NULL,
    sx INTEGER UNSIGNED NOT NULL,
    dx INTEGER UNSIGNED NOT NULL,
    PRIMARY KEY(id)
);

Nota: in MySQL le parole "left" e "right" sono keywords riservate, per cui è possibile utilizzarle come nomi di colonna solo racchiudendole all'interno dei backtick (l'apice rovesciato, ASCII 96), quindi ad esempio `left` e `right`. Per evitare questo fastidio, molti tutorial in inglese utilizzano le abbreviazioni "lft" e "rgt", mentre noi abbiamo preferito "sx" e "dx" che dovrebbero essere di uguale comprensione.

Sempre prendendo spunto da altri tutorial, possiamo trovare diverse implementazioni che inseriscono nella tabella un campo per tenere traccia dell'identificativo del padre per ciascun record, oppure che inseriscono un campo per tenere traccia del livello di ciascun record (1 per la radice, poi proseguendo attraverso l'albero questo numero aumenta). Per ragioni di semplicità, abbiamo proposto la versione più basilare del Modified Preorder Tree Traversal Algorithm, che necessita soltanto delle due etichette numerate. Anche la scelta di una chiave AUTO_INCREMENT è dovuta a motivi di comodità.

Inseriamo ora la struttura aziendale, mantenendo i riferimenti numerici indicati in figura 6:

INSERT INTO personale (nome, sx, dx) VALUES ('Massimiliano', 1, 14), ('Francesco', 2, 13), ('Mario', 3, 4),('Luigi', 5, 6), ('Fabio', 7, 12), ('Piero', 8, 9), ('Gianni', 10, 11);

Abbiamo inserito "manualmente" i valori per i campi sx e dx, soltanto per semplicità visto che i numeri erano già noti. Nei prossimi inserimenti vedremo come sia relativamente semplice calcolare i valori per le nuove etichette.

Finalmente siamo pronti per lavorare sulla tabella.

Operazioni sulla tabella

La fatica iniziale per comprendere questo tipo di soluzione ci ripaga ora che stiamo per affrontare la pratica.

Per godere a pieno dei vantaggi offerti dall'algoritmo esaminato, si potrebbero sfruttare alcune peculiarità del linguaggio SQL che sono state introdotte soltanto di recente in MySQL. Come qualcuno avrà intuito, il riferimento riguarda soprattutto le subquery, che prima della versione 4.1 di MySQL non erano presenti, pur essendo parzialmente emulabili (o meglio, riscrivibili) con delle self join.

Andiamo ora al sodo: l'Adjacency List Model mostrava la sua debolezza nella necessità di effetuare una query per ogni livello dell'albero. Aumentando i livelli, aumenta anche il numero di SELECT da eseguire, ed aumenta quindi il carico al sistema. Con il nostro nuovo approccio, dotrebbe bastarci una sola query. Se vogliamo, ad esempio, scoprire il percorso necessario per andare dalla radice (Massimiliano) al nodo "Piero", dobbiamo selezionare i record che abbiano rispettivamente l'etichetta sinistra con valori inferiori e l'etichetta destra con valori superiori rispetto a quelle di Piero.

Ecco la query:

SELECT nome FROM personale WHERE sx <= 8 AND dx >= 9

La scelta degli operatori <= e >= rispetto a < e > ci permette di includere Piero nei risultati della query.

Supponiamo però di non conoscere i valori delle due etichette legate a Piero, ma di conoscerne soltanto la chiave primaria (id=6 ). In questo caso le possibilità sono due, che potete testare sulle diverse versioni di MySQL in base alla disponibilità o meno delle subselect:

-- Subquery disponibili, versione >= 4.1
SELECT nome FROM personale
WHERE sx <= (SELECT sx FROM personale WHERE id=6)
AND dx >= (SELECT dx FROM personale WHERE id=6);

Se le subquery non sono disponibili, saranno necessarie due query, per conoscere i valori dei campi sx e dx. Un esempio di pseudocodice:

$sx, $dx = SELECT sx, dx FROM personale WHERE id=6;
SELECT nome FROM personale WHERE sx <= $sx AND dx >= $dx ORDER BY sx ASC;

Quest'ultima soluzione funziona sulle versioni più vecchie di MySQL (3.23.*) ed è implementabile con poche righe di PHP; troviamo un esempio nella funzione ns_get_path() della libreria allegata. Utilizzando il seguente "trucchetto", possiamo riscrivere la selezione per appoggiarci ancora ad un'unica SELECT, pur non disponendo di subquery:

SELECT A.nome AS nome
FROM personale AS A, personale AS B
WHERE A.sx <= B.sx AND A.dx > B.dx AND B.id=6 ORDER BY sx ASC;

È infine possibile riscrivere ulteriormente la query, utilizzando il costrutto BETWEEN, mantenendo in tutti i casi la compatibilità con le versioni 3.23.* di MySQL. Il costo di queste selezioni risulta comunque essere molto simile, per cui nella libreria abbiamo adottato, senza pensarci troppo, il primo sistema. Ecco un esempio di codice che sfrutta la funzione citata poco sopra:

<?php
// Inclusioni necessarie
require_once 'mysqlconnect.php';
require_once 'nestedset.php';
// Piero, id=6
$id = 6;
$path = ns_get_path($id);
// Stampo il percorso dalla radice a Piero
foreach ($path as $p) {
	echo "- {$p} ";
}
?>

Questo codice andrà a stampare "- Massimiliano - Francesco - Fabio - Piero". È importante notare come, all'aumentare del numero di livelli, le query rimangano sempre due.

Per quanto riguarda eventuali manipolazioni sull'albero, le operazioni sono leggermente più complicate e necessitano di più query, sempre comunque in numero fisso e non influenzabile dal numero di livelli. Nella libreria di esempio analizziamo la possibilità di inserire o eliminare un nodo, rispettivamente con le funzioni ns_insert_node() e ns_delete_node(). Proviamo per esempio ad inserire un nuovo impiegato, sotto le dipendenze di Piero (id=6):

<?php
// Includsioni necessarie
require_once 'mysqlconnect.php';
require_once 'nestedset.php'
// Piero, id=6
$id = 6;
// Il nome del nuovo impiegato
$nome = 'Marco';
ns_insert_node($id, $nome);
// Visualizzo il percorso dalla radice al nuovo impiegato
$path = ns_get_path(mysql_insert_id());
foreach ($path as $p) {
	echo "- {$p} ";
}
?>

Questo esempio ripropone il percorso visto nel codice precedente, aggiungendo il nodo "Marco" alla fine. Per comodità sfruttiamo mysql_insert_id(), una funzione che permette di recuperare l'ultimo valore di tipo AUTO_INCREMENT inserito, nel nostro caso quello di "Marco" appunto.

A questo punto è consigliato lo studio delle funzioni proposte della libreria, tenendo presente che anche questa volta il codice è stato estremamente semplificato, togliendo eventuali controlli sugli input o sugli errori che possono insorgere ed inquadrando da vicino la tabella creata in precedenza. Per poter riutilizzare la libreria sarà ovviamente necessario apportare dei piccoli aggiustamenti.

Considerazioni sul Modified Preorder Tree Traversal

L'approccio non è banale e può inizialmente scoraggiare. La struttura "ad etichette", apparentemente superflua o contorta, fornisce però alcuni vantaggi in termini di rapidità di accesso alle informazioni.

Abbiamo visto come una sola query SELECT possa fornirci tutto il percorso dalla radice ad un determinato nodo. Abbiamo visto come la numerazione delle etichette abbia un senso: le foglie hanno due numeri consecutivi, mentre la radice da una parte ha il numero 1, dall'altra ha il doppio dei nodi totali. Inoltre, ciascun nodo ha l'etichetta sinistra con valore maggiore rispetto al padre e l'etichetta destra invece con valore inferiore.

E se volessimo sapere quanti nodi si trovano sotto ad un determinato record? Basta un po' di matematica: (dx - sx - 1)/2 è la soluzione al nostro quesito, ed ecco come recuperare questa informazione, ad esempio, per il nodo "Francesco" (id=2):

SELECT ROUND( (dx-sx-1)/2 , 0) FROM personale WHERE id=2;

Dove ROUND() è una funzione di MySQL che diventa necessaria per avere risultati interi (lo zero posto come secondo parametro è il numero di cifre dopo la virgola).

Considerazioni finali e link

Probabilmente non abbiamo risposto a tutte le domande. Le possibili implementazioni in grado di risolvere il nostro problema sono molte, e talvolta è difficile scegliere. Stando a quanto abbiamo visto, il Modified Preorder Tree Traversal è un algoritmo che ci garantisce buone prestazioni rispetto all'Adjacency List Model soprattutto quando i livelli dell'albero sono parecchi, e quando abbiamo bisogno di frequenti selezioni come quelle analizzate. Nel caso in cui capiti spesso di manipolare l'albero, un approccio di questo tipo risulta forse più scomodo. Comodità o efficienza? È questa la scelta che viene lasciata al programmatore.

Concludiamo con una carrellata veloce di link sull'argomento:

• Articolo su Sitepoint, che ha dato il via alla mia ricerca di informazioni sull'argomento; non è particolarmente esaustivo, ma è una discreta base per confrontare Adjacenct List e Nested Sets
• Articolo su Evolt.org, che confronta alcuni metodi per gestire strutture gerarchiche su database.
• Ottima classe PHP che implementa i Nested Set, compatibile con PEAR (richiede PEAR::DB)
• La parola a Joe Celko, che ci parla di alberi in SQL.

Infine, non si possono non citare due famosi scritti dello stesso Celko: "SQL for Smarties", noto libro in cui Celko parla di SQL a 360 gradi, dedicando ben due capitoli alla rappresentazione di strutture gerarchiche su database, da cui poi è derivato il più recente "Trees and Hierarchies in SQL for Smarties", circa 200 pagine interamente dedicate all'argomento.